2017年九年级上学期开学考试卷数学卷（解析版）

九年级上期开学考试

数 学 试 卷

 

考试时间：60分钟

一、选择题（3×10=30分）

1．下列方程①；②；③中，是一元二次方程有（    ）

A．①②       B．①③        C．②③        D．③

【答案】B.

考点：一元二次方程的定义.

2．矩形具有而菱形不具有的性质是（  ）

A．两组对边分别平行       B．对角线相等

C．对角线互相平分         D．两组对角分别相等

【答案】B.

【解析】

试题分析：选项A，矩形与菱形的两组对边都分别平行，选项A错误；选项B，矩形的对角线相等，菱形的对角线不相等，选项B正确；选项C，矩形与菱形的对角线都互相平分，选项C错误；选项D，矩形与菱形的两组对角都分别相等，选项D错误．故答案选B.

考点：矩形的性质；菱形的性质.

3.用配方法解一元二次方程x²+4x-5=0，此方程可变形为（   ）

A．（x+2）²=9    B．（x-2）²=9        C．（x+2）²=1        D．（x-2）²=1

【答案】A,

【解析】

试题分析：把常数项-5移项后，应该在左右两边同时加上一次项系数4的一半的平方,即x²+4x-5=0，x²+4x=5，x²+4x+4=9，（x+2）²=9，故答案选A.

考点：配方法解一元二次方程.

4．在菱形ABCD中，对角线AC长为3cm，∠ABC=60°，则菱形ABCD的周长为（ ）．

A．6cm       B．12cm       C．12cm        D．24cm

【答案】C.

【解析】

试题分析：由菱形的性质可得AB=BC,又因∠ABC=60°，可得△ABC为等边三角形，所以AB=BC=AC=3cm，从而得菱形ABCD的周长为3×4=12cm.故答案选C.

考点：菱形的性质；等边三角形的判定及性质.

5．若方程x²－3x－2=0的两实根为x₁，x₂，则（x₁＋2）（x₂＋2）的值为（  ）

A、－4         B、6          C、8           D、12[

【答案】C.

【解析】[来源:学+科+网]

试题分析：方程x²－3x－2=0的两实根为x₁，x₂，由一元二次方程根与系数的关系可得x₁+x₂=3，x₁●x₂=-2，所以（x₁＋2）（x₂＋2）=x₁●x₂+2（x₁+x₂）+4=-2+6+4=8，故答案选C.学科网

考点：一元二次方程根与系数的关系.

:

6．如图，在四边形ABCD中，E、F、G、H分别是AB、BD、CD、AC的中点，要使四边形EFGH是菱形，则四边形ABCD只需要满足一个条件，是（    ）

 A．四边形ABCD是梯形    B．四边形ABCD是菱形

C．对角线AC=BD          D．AD=BC

【答案】D.

【解析】

试题分析：在四边形ABCD中，E、F、G、H分别是AB、BD、CD、AC的中点，根据三角形的中位线定理易证四边形EFGH是平行四边形；要使平行四边形EFGH是菱形，只需使GH=GF即可，根据三角形的中位线定理可得GH=AD,GF=BC,所以当AD=BC时，可得GH=GF，平行四边形EFGH是菱形，故答案选D.

考点：三角形的中位线定理;菱形的判定定理.

7．已知a、b是一元二次方程的两根，那么的值为（     ）

A．    B．         C．         D．

【答案】D.

考点：一元二次方程根与系数的关系.

8．如图，在菱形ABCD中，AB=5，对角线AC=6．若过点A作AE⊥BC，垂足为E，则AE的长为（  ）．

  A．4        B．        C．        D．5

]

【答案】C.

【解析】

试题分析：如图，连接BD，交AC于O点，根据菱形的性质可得AB=BC=5cm，OA=OC,OB=OD,AC⊥BD,在Rt△AOB中，根据勾股定理求得OB=4cm，所以BD=8cm.再由,代入数值即可得AE=,故答案选C.

考点：菱形的性质；勾股定理.

9．如图所示，在一边靠墙（墙足够长）的空地上，修建一个面积为640m²的矩形临时仓库，仓库一边靠墙，另三边用总长为80 m的栅栏围成，若设栅栏AB的长为xm，则下列各方程中，符合题意的是（    ）

A．          B．

C．           D．

【答案】A.

【解析】

试题分析：设栅栏AB的长为xm,根据题意可得BC=（80-x），再根据矩形的面积公式可列方程．故答案选A.学科网

考点：一元二次方程的应用.

10．如图，两个正方形边长分别为a、b，a+b=16，ab=48，图中阴影部分的面积为（     ）．

A．56      B．72       C．80       D．104

【答案】A.

【解析】

试题分析:观察图形可得图中阴影部分的面积为[来源:学§科§网]

=，把a+b=16，ab=48，代入可得原式=，故答案选A.

考点：完全平方公式的应用.

二、填空题（3×8=24分）

1．若一元二次方程x²﹣x+k=0有实数根，则k的取值范围是       ．

【答案】k≤.

考点：一元二次方程根的判别式.

2．若矩形ABCD的两邻边长分别为一元二次方程的两个实数根，则矩形ABCD的对角线长为      ．

【答案】5.

【解析】

试题分析：矩形ABCD的两邻边长分别为一元二次方程的两个实数根，解这个方程可得，即矩形ABCD的两邻边长分别为3和4，由勾股定理求得对角线的长为5.

考点：一元二次方程的解法；勾股定理；矩形的性质.

3．已知（x²＋y²）（x²＋y²－1）－12=0，则x²＋y²的值是            ．

【答案】4.

【解析】

试题分析：设x²＋y²=m，方程（x²＋y²）（x²＋y²－1）－12=0可化为m（m-1）-12=0，解得，又因x²＋y²＞0，所以x²＋y²=4.

考点：换元法解一元二次方程.

4．在菱形ABCD中，已知菱形ABCD的周长是40，AC=12，则菱形ABCD的面积为     ．

【答案】96.

【解析】

试题分析：已知菱形ABCD的周长为40，可得菱形的边长AB=10，根据菱形的性质可得OA=OC=6，AC⊥BD,所以△ABO为直角三角形，由勾股定理可得OB=8，即可得BD=16，所以菱形ABCD的面积为.

考点：菱形的性质；勾股定理.

5．如图，在一块长为22米，宽为17米的矩形地面上，要修建同样宽的两条互相垂直的道路（两条道路分别与矩形的一条边平行），剩余部分种上草坪，使草坪面积为300平方米，设道路宽为x米，根据题意可列出的方程为               ．

【答案】（22-x）（17-x）=300.

考点：一元二次方程的应用.

6．如图正方形ABCD中，∠DAF=25⁰，AF交对角线BD于点E，连接EC， 则∠BCE=______。

【答案】65⁰.

【解析】

试题分析：根据已知条件，利用SAS易证△AED≌△CED,根据全等三角形的性质可得∠DAF=∠DCE=25⁰，所以∠BCE=∠BCD-∠DCE=90⁰-25⁰=65⁰.

考点：正方形的性质；全等三角形的判定及性质.

7．设是方程的两个实数根，则的值为            ．

【答案】2008.

【解析】

试题分析：已知a是方程的实数根，可得，即，由一元二次方程根与系数的关系可得a+b=-1，所以==2009-1=2008.

考点：一元二次方程的解；一元二次方程根与系数的关系.

8．如图，矩形ABCO中，OA在x轴上，OC在y轴上，且OA=2，AB=5，把△ABC沿着AC对折得到△AB′C，AB′交y轴于D点，则D点的坐标为                  ．

【答案】（0,2.1）.

【解析】

试题分析：由折叠的性质可得∠BAC＝∠CAD,由平行线的性质可得∠BAC＝∠ACD,所以∠CAD＝∠ACD,根据等腰三角形的性质可得AD=CD,设OD=x，则AD=CD=5-x，在Rt△AOD中，由勾股定理得，解得x=2.1，所以D点的坐标为（0,2.1）.

考点：折叠的性质；等腰三角形的性质；勾股定理；坐标与图形.

三、计算题（20分）

1.（10分）解方程

（1）x（x＋2）=5x＋10           （2）3x²－6x＋1=0

【答案】(1)=-2，=5；（2）.

（2）3x²－6x＋1=0

a=3，b=-6，c=1

∴△=36-4×3×1=36-12=24＞0

∴x=

∴

考点：一元二次方程的解法.

2.（10分）已知关于x的一元二次方程．

（1）若此方程有两个不相等的实数根，求实数k的取值范围；

（2）已知x=3是此方程的一个根，求方程的另一个根及k的值；

【答案】(1)k＜2；(2)k=-2,方程的另一个根为-1.

【解析】

试题分析：（1）利用一元二次方程根的判别式即可得到关于k的不等式，从而求解；（2）根据一元二次方程根与系数的关系即可求解．

试题解析：（1）∵方程有两个不相等的实数根，

∴△=4-4（k-1）＞0，即-4k+8＞0，解得k＜2；

（2）设方程的两个根分别为=3，，由一元二次方程根与系数的关系可得，+=2，即可得=-1.

把=3代入方程，解得k=-2.

考点：一元二次方程根的判别式；一元二次方程根与系数的关系.

四、解答题（26分）

１．（14分）已知：如图，在矩形ABCD中，M，N分别是边AD，BC的中点，E，F分别是线段BM，CM的中点．

（1）求证：△ABM≌△DCM；

（2）判断四边形MENF是什么特殊四边形，并证明你的结论；

（3）当AD：AB=            时，四边形MENF是正方形（只写结论，不需证明）．

 

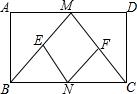
【答案】(1)详见解析；（2）四边形MENF是菱形，证明见解析；（3）当AD∶AB＝2∶1时，四边形MENF是正方形．

【解析】

试题分析：（1）根据SAS即可证明△ABM≌△DCM；（2）由（1）得出BM=CM，再根据三角形的中位线定理得出EN=MF，EM=FN，先证四边形MENF是平行四边形，再证ME＝MF，从而可得平行四边形MENF是菱形；（3）当AD∶AB＝2∶1时，四边形MENF是正方形．可以利用正方形的性质得到MA=AB=MD，从而确定AD：AB的值．

试题解析：(1)证明：∵四边形ABCD是矩形，

∴AB＝DC，∠A＝∠D＝90°，

∵M为AD中点，∴AM＝DM，

在△ABM和△DCM，

∴△ABM≌△DCM(SAS)；

(2)

(3)解：当AD∶AB＝2∶1时，四边形MENF是正方形．理由是：

∵四边形MENF是正方形，[来源:学科网ZXXK]

∴∠EMF=90°，

由（1）知：Rt△ABM≌Rt△DCM（SAS），

∴∠AMB=∠DMC=45°，[来源:学科网]

此时MA=MD=DC，

∴AD=2DC，即AD∶AB＝2∶1.

考点：全等三角形的判定及性质；菱形的判定；正方形的判定.

2.（12分）商场某种商品平均每天可销售30件，每件盈利50元。为了尽快减少库存，商场决定采取适当的降价措施。经调查发现，每件商品每降价1元，商场平均每天可多售出2件。设每件商品降价x元。据此规律，请回答：[来源:学科网ZXXK]

（1）商场日销售量增加       件，每件商品盈利       元（用含x的代数式表示）；

（2）在上述条件不变、销售正常情况下，每件商品降价多少元时，商场日盈利可达到2100元？

【答案】（1）2x,（50－x）；（2）x＝20.

【解析】

试题分析：（1）由题意可知，降价1元，可多售出2件，降价x元，可多售出2x件，每件商品盈利的钱数＝原来的盈利－降低的钱数即可得每件商品盈利的钱数；（2）根据等量关系“每件商品的盈利×可卖出商品的件数＝2100”，把相关数值代入计算得到合适的解即可．

试题解析：（1）降价1元，可多售出2件，降价x元，可多售出2x件，盈利的钱数＝50－x，故答案为2x；（50－x）；

（2）由题意得：（50－x）（30＋2x）＝2100，

化简得：x²－35x＋300＝0，

解得：x₁＝15，x₂＝20．
∵该商场为了尽快减少库存，则x＝15不合题意，舍去．

∴x＝20．

答：每件商品降价20元，商场日盈利可达2100元．学科网

考点：一元二次方程的应用.